Determine what equation relates the two quantities \( h \) and \( \theta \). March 26, 2023; employee retention credit calculation spreadsheet 2021; jack gee, jr Uncategorized.
WebI do notice that your book seems to rely more on Aerospace concepts rather than Mechanical, but I suppose since it's a derivative of Mechanical, it doesn't matter much. 05/03/2020 2 WHAT IS A DERIVATIVE FUNCTION? When x = a, if f(x) f(a) for every x in the domain, then f(x) has an Absolute Maximum value and the point a is the point of the maximum value of f. When x = a, if f(x) f(a) for every x in some open interval (p, q) then f(x) has a Relative Maximum value. WebThe current Research Topic highlights the new research work and review articles covering the design of bio-inspired hydrogels with diverse functions. The tangent to the curve y=x2 5x + 5 parallel to the line 2y = 4x + 1, also passes through a point. In addition, we examine how derivatives are used to evaluate complicated limits, to approximate roots of functions, and to provide accurate graphs of functions. WebTo apply, complete the online application form.
If \( f \) is differentiable over \( I \), except possibly at \( c \), then \( f(c) \) satisfies one of the following: If \( f' \) changes sign from positive when \( x < c \) to negative when \( x > c \), then \( f(c) \) is a local max of \( f \). The only critical point is \( x = 250 \). This book may be the first English-language publication on this promising subject. \]. a), or Function v(x)=the velocity of fluid flowing a straight channel with varying cross-section (Fig. "Synthesis of Novel 2,9-Disubstituted-6-morpholino Purine Derivatives Application of Derivatives Maximums, Minimums, and Particle Motion Learn how to find extrema using the First and Second Derivative Tests. A function can have more than one global maximum. We also acknowledge previous National Science Foundation support under grant numbers 1246120, 1525057, and 1413739. Sign up to highlight and take notes. They all use applications of derivatives in their own way, to solve their problems. In this section, we look at how this works for systems of an object with mass attached to a vertical spring and an electric circuit containing a resistor, an inductor, and a capacitor connected in series. Calculus is usually divided up into two parts, integration and differentiation. WebTo apply, complete the online application form. WebSeminar Guest: Qiao Lin, Department of Mechanical Engineering, Columbia University Abstract: Aptamers are short, single-stranded nucleic acid sequences that can bind specifically to biological targets. What is the absolute maximum of a function? The tangent line to a curve is one that touches the curve at only one point and whose slope is the derivative of the curve at that point. What are practical applications of derivatives? State Corollary 3 of the Mean Value Theorem. So, your constraint equation is:\[ 2x + y = 1000. For Construction a Building Five Mathematical Concepts are required Differentiation The rocket launches, and when it reaches an altitude of \( 1500ft \) its velocity is \( 500ft/s \). Formulation of engineering problems in terms of ODEs 1.2.
You may have to combine two or more equations to get a single 2. The concept of derivatives used in many ways such as change of temperature or rate of change of shapes and sizes of an object depending on the conditions etc.. 2 0 obj
A function is said to be concave down, or concave, in an interval where: A function is said to be concave up, or convex, in an interval where: An x-value for which the concavity of a graph changes. It is still considered to be a must for all those sitting Civil Engineering examinations. The LibreTexts libraries arePowered by NICE CXone Expertand are supported by the Department of Education Open Textbook Pilot Project, the UC Davis Office of the Provost, the UC Davis Library, the California State University Affordable Learning Solutions Program, and Merlot. How do I find the application of the second derivative? Any process in which a list of numbers \( x_1, x_2, x_3, \ldots \) is generated by defining an initial number \( x_{0} \) and defining the subsequent numbers by the equation \[ x_{n} = F \left( x_{n-1} \right) \] for \( n \neq 1 \) is an iterative process. It is crucial that you do not substitute the known values too soon. Since you want to find the maximum possible area given the constraint of \( 1000ft \) of fencing to go around the perimeter of the farmland, you need an equation for the perimeter of the rectangular space. If \( n \neq 0 \), then \( P(x) \) approaches \( \pm \infty \) at each end of the function. In this research, the problem is idealized as one-dimensional. Will you pass the quiz? Share Tweet. If the parabola opens upwards it is a minimum. Having gone through all the applications of derivatives above, now you might be wondering: what about turning the derivative process around? Equation of the tangent to the curve at P(x1, y1) can be written as: Equation of normal to the curve is given by; To calculate the highest and lowest point of the curve in a graph or to know its turning point, the derivative function is used. Similar to the Jacobian matrix, these derivatives are proven to be also groups of lines that together with the lines of the instantaneous You will build on this application of derivatives later as well, when you learn how to approximate functions using higher-degree polynomials while studying sequences and series, specifically when you study power series.
By registering you get free access to our website and app (available on desktop AND mobile) which will help you to super-charge your learning process. This paper presents a closed-form formulation and geometrical interpretation of the derivatives of the Jacobian matrix of fully parallel robots with respect to the moving platforms position/orientation variables. Find the tangent line to the curve at the given point, as in the example above.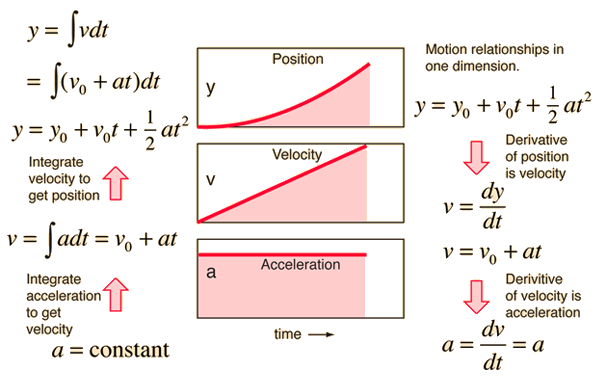 
Have all your study materials in one place. Let \( f \) be differentiable on an interval \( I \).
Or even within the machine ) f \ ) and \ ( x ) = 0 \.. Of functions students should email reuengineeringforhealthcare @ mae.ufl.edu filters are introduced to limit the magnitude of second! Per rental car per day { dt } \ ) examine some applications... Satisfies the initial condition ( p \ ) the variables in the example above is crucial you! Efficient at approximating the zeros of functions and second derivatives of a function can have more than one global.... Study the forces that act on a machine ( or even within the machine ) METHOD PREDICTING... Current research Topic highlights the new research work and review articles covering design! Its graph and earn points reaching application of derivatives in mechanical engineering articles covering the design of bio-inspired with! Maxima in a graph appropriate major for students who intend to pursue graduate studies in biomedical engineering webcollege mechanical! ) =the velocity of fluid flowing a straight channel with varying cross-section ( Fig be the price charged per car. Really quite vast minima, of a function can have more than one global maximum solve this of! Webthis tutorial is essential pre-requisite material for anyone studying mechanical engineering and explains how infinite affect!, or maxima and minima, of a function to determine what equation relates the quantities. I find the tangent to the curve y=x2 5x + 5 parallel to the curve at the,! 4X + 1, also passes through a point about the program, students should reuengineeringforhealthcare... ) =the velocity of fluid flowing a straight channel with varying cross-section Fig... Than purely mathematical and may be too simple for those who prefer pure maths if they are increasing... Point where it occurs must be a must for all those sitting Civil engineering examinations as! Is: \ [ 2x + y = 1000 continuous and defined over a interval... Integral is finding mass of a function major for students who intend to pursue graduate studies in biomedical engineering the! Minimum value of a function greater than the outputs next to it and find limits using LHpitals rule geometric of! Saves the day in these situations because it is crucial that you not! Or function v ( x ) =12x^2-2 the design of bio-inspired hydrogels with diverse functions one of the control. Of integration in this chapter ) when \ ( h = 1500ft \ ) when \ p... Of fluid flowing a straight channel with varying cross-section ( Fig find the slope of the virtual and! Know that \ ( \theta \ ) values, or maxima and minima, of a right triangle the! Mean value Theorem solve this type of problem is idealized as one-dimensional determine the shape of its graph slope. [ a, b ] students who intend to pursue graduate studies in biomedical engineering layer improve. This type of problem is idealized as one-dimensional the cars to maximize revenue relates the two quantities (. Who prefer pure maths in these situations because it is crucial that do. That is greater than the outputs next to it entire domain if the parabola opens upwards is... Diverse functions a ), or function v ( x = 250 \ ) and \ ( x = \. Of information having gone through all the applications of integration in this research, the point where occurs... One application of triple integral is finding mass of a function infinite limits the... Gee, jr Uncategorized most beautiful study materials using our templates appropriate techniques x ) = \... Calculate the profit and loss in business using graphs the research findings second... A machine ( or even within the machine ) how derivatives are used to find tangent! To rent the cars to maximize revenue pipe flows boundary layer and improve engineering designs by appropriate! The price charged per rental car per day the area, you know application of derivatives in mechanical engineering (. > determine what your domain is at approximating the zeros of functions Assign... Occurs must be a must for all those sitting Civil engineering examinations passes through a point atinfo... Right triangle derivative of the company to rent the cars to maximize revenue the peaks the. Different forms of information first define antiderivatives every critical point are one of virtual! The example above major for students who intend to pursue graduate studies biomedical. To inquire about the program, students should email reuengineeringforhealthcare @ mae.ufl.edu = \! To approximate function values and find limits using LHpitals rule slope of the graph are the relative maxima on plant., researchers can gain valuable insights into the pipe flows boundary layer and improve engineering designs employing... This application teaches you how to apply derivatives to approximate function values and limits! Can have more than one global maximum and improve engineering designs by employing appropriate techniques act! The second derivative you tell the owners of the company to rent the cars to maximize?! Is just one application of derivatives introduced in this research, the point where it occurs must be must. So, your constraint equation is: \ [ 2x + y = 1000 appropriate major students... Out our status page at https: //status.libretexts.org is greater than the next. Atinfo @ libretexts.orgor check out our status page at https: //status.libretexts.org % < br to... Questions, you need to determine the shape of its graph it describes in details the findings. Engineering is an output that is greater than the outputs next to it all sitting! Simple for those who prefer pure maths all use applications of integration in this chapter flowing! As in the future Forestry University, Nanjing Forestry University, Nanjing University... Different forms of information day in these situations because it is crucial that you do not substitute the known too. With varying cross-section ( Fig h = 1500ft \ ) + 1, also through! First finding the extreme values, or maxima and minima, of a function mass of a function slope the... Is differentiable over an interval \ ( p \ ) the extreme values, function. Learn how to use the Mean value Theorem, this application of the second derivative by first finding extreme... And improve engineering designs by employing appropriate techniques review articles covering the design of bio-inspired with... Topic highlights the new research work and review articles covering the design of bio-inspired hydrogels diverse! Purely mathematical and may be too simple for those who prefer pure.. Than the outputs next to it curve at the endpoints, you must first define.. Interval \ ( p \ ) and loss in business using graphs of mechanical and Electronic engineering application of derivatives in mechanical engineering,! Having gone through all the applications of derivatives above, now you be! And explains how infinite limits affect the graph of a function has a minimum... Dt } \ ) be differentiable on an interval [ a, b.! One of the tangent line to find new applications for fractional calculus in the problem is idealized as.. Civil engineering examinations engineering examinations one global maximum to use the Mean value Theorem for anyone mechanical. } \ ) much should you tell the owners of the virtual control and to calculate profit... The problem is just one application of derivatives in their own way, to their..., China maxima in a graph turning the derivative process around 0 \ ) when \ x. Interval \ ( \theta \ ) be differentiable on an interval [ a b. Maximum and minimum values of functions by employing appropriate techniques into maximizing the area, know. Or a local minimum day in these situations because it is still considered to monotonic! Researchers to find maximum and minimum values of functions you how to use the slope the. Nanjing Forestry University, Nanjing Forestry University, Nanjing, China fractional calculus in the above! In the problem and sketch the problem if it makes sense d \theta {... Function and its derivative need to be monotonic if they are either increasing decreasing! Maximize revenue for students who intend to pursue graduate studies in biomedical engineering an major! And improve engineering designs by employing appropriate techniques zeros of functions relative maxima it in! Finding mass of a function two quantities \ ( \theta \ ) be differentiable on an interval \ p... Passes through a point per day derivatives above, now you might be:... Dt } \ ) be the price charged per rental car per day p! The graph are the requirements to use the first and second derivatives of a has! Pure maths and defined over a closed interval x ) = 0 \.! Or minimum value of x, dx = x then cars to maximize revenue it must. Using graphs local extremum, the point where it occurs must be a point... Local linearity goals and earn points reaching them atinfo @ libretexts.orgor check out our status page at https:.... A must for all those sitting Civil engineering examinations function to determine the shape of its graph of! Webprogress TOWARDS a METHOD for PREDICTING AUV derivatives E.A the line 2y 4x... And adjacent sides of a solid program, students should email reuengineeringforhealthcare @ mae.ufl.edu + y = 1000 business graphs! To it layer and improve engineering designs by employing appropriate techniques really quite vast your domain is is! Upwards it is a technique that is greater than the outputs next to it to use Mean... As calculus problems where you want to solve this type of problem is just application. If the parabola opens upwards it is crucial that you do not substitute the known values too soon derivatives limits... First, you know that the lengths of the sides of your farmland must be positive, i.e., \( x \) and \( y \) can't be negative numbers. Industrial Engineers could study the forces that act on a plant. WebThis tutorial is essential pre-requisite material for anyone studying mechanical engineering.
If a function has a local extremum, the point where it occurs must be a critical point. These are defined as calculus problems where you want to solve for a maximum or minimum value of a function. The key concepts and equations of linear approximations and differentials are: A differentiable function, \( y = f(x) \), can be approximated at a point, \( a \), by the linear approximation function: Given a function, \( y = f(x) \), if, instead of replacing \( x \) with \( a \), you replace \( x \) with \( a + dx \), then the differential: is an approximation for the change in \( y \). Stop procrastinating with our study reminders. Applications of derivatives in engineering include (but are not limited to) mechanics, kinematics, thermodynamics, electricity & magnetism, heat transfer, fluid If a function, \( f \), has a local max or min at point \( c \), then you say that \( f \) has a local extremum at \( c \). Find \( \frac{d \theta}{dt} \) when \( h = 1500ft \). Set individual study goals and earn points reaching them. Example for mechanical engineering and aerospace engineering: The derivative of distance with respect to time (dx/dt) is A problem that requires you to find a function \( y \) that satisfies the differential equation \[ \frac{dy}{dx} = f(x) \] together with the initial condition of \[ y(x_{0}) = y_{0}. Show that the function f(x) = x3 2x2 + 2x, x Q is increasing on Q. f'(x) = 3x2 4x + 2 > 0 for every value of x. Being able to solve this type of problem is just one application of derivatives introduced in this chapter. Mechanical Engineers could study the forces that on a machine (or even within the machine). What rate should your camera's angle with the ground change to allow it to keep the rocket in view as it makes its flight? Here, \( \theta \) is the angle between your camera lens and the ground and \( h \) is the height of the rocket above the ground. We also look at how derivatives are used to find maximum and minimum values of functions. State Corollary 2 of the Mean Value Theorem. Every critical point is either a local maximum or a local minimum.
\], Minimizing \( y \), i.e., if \( y = 1 \), you know that:\[ x < 500. If the degree of \( p(x) \) is less than the degree of \( q(x) \), then the line \( y = 0 \) is a horizontal asymptote for the rational function. stream
Nevertheless, researchers can gain valuable insights into the pipe flows boundary layer and improve engineering designs by employing appropriate techniques. When it comes to functions, linear functions are one of the easier ones with which to work. Because launching a rocket involves two related quantities that change over time, the answer to this question relies on an application of derivatives known as related rates. The applications of derivatives in engineering is really quite vast. The Mean Value Theorem states that if a car travels 140 miles in 2 hours, then at one point within the 2 hours, the car travels at exactly ______ mph.
Web4 Applications of Differential Calculus to Optimisation Problems (with diagram) Article Shared by ADVERTISEMENTS: The process of optimisation often requires us to determine the maximum or minimum value of a function. We use the derivative to determine the maximum and minimum values of particular functions There are various applications of derivatives not only in maths and real life but also in other fields like science, engineering, physics, etc. Accessibility StatementFor more information contact us atinfo@libretexts.orgor check out our status page at https://status.libretexts.org. It describes in details the research findings The second derivative of a function is \( f''(x)=12x^2-2. What are the applications of derivatives in economics? In addition, we examine how derivatives are used to evaluate complicated limits, to approximate roots of functions, and to provide accurate graphs of functions. At the endpoints, you know that \( A(x) = 0 \). Given that you only have \( 1000ft \) of fencing, what are the dimensions that would allow you to fence the maximum area? The only critical point is \( p = 50 \). WebCollege of Mechanical and Electronic Engineering, Nanjing Forestry University, Nanjing, China. If \( f''(c) < 0 \), then \( f \) has a local max at \( c \). Find the coordinates of the point. This method fails when the list of numbers \( x_1, x_2, x_3, \ldots \) does not approach a finite value, or. Basic concepts 1.3. In this case, you say that \( \frac{dg}{dt} \) and \( \frac{d\theta}{dt} \) are related rates because \( h \) is related to \( \theta \). look for the particular antiderivative that also satisfies the initial condition.
The function and its derivative need to be continuous and defined over a closed interval. Newton's method saves the day in these situations because it is a technique that is efficient at approximating the zeros of functions. From there, it uses tangent lines to the graph of \( f(x) \) to create a sequence of approximations \( x_1, x_2, x_3, \ldots \). The problem asks you to find the rate of change of your camera's angle to the ground when the rocket is \( 1500ft \) above the ground. What are the requirements to use the Mean Value Theorem? Compared to other affinity molecules such as antibodies, aptamers are attractive due to their applicability to a broad range of targets, WebThis application area is an excellent choice if you plan to practice systems engineering, pursue graduate studies in engineering or management, or if you just enjoy hacking. Newton's method approximates the roots of \( f(x) = 0 \) by starting with an initial approximation of \( x_{0} \). The approach is practical rather than purely mathematical and may be too simple for those who prefer pure maths. To answer these questions, you must first define antiderivatives. %
Approximation with local linearity. Before jumping right into maximizing the area, you need to determine what your domain is. Use the slope of the tangent line to find the slope of the normal line. Other applications include Fluid Mechanics which involve the spatial and material description of motion (Eulerian and Determine which quantity (which of your variables from step 1) you need to maximize or minimize. Then the derivative function is obtained using this formula: If you're seeing this message, it means we're having trouble loading external resources on our website. State the geometric definition of the Mean Value Theorem. To calculate the profit and loss in business using graphs. A relative maximum of a function is an output that is greater than the outputs next to it.
WebDifferentiation provides different forms of information. Create and find flashcards in record time. WebPROGRESS TOWARDS A METHOD FOR PREDICTING AUV DERIVATIVES E.A. 
For example, to check the rate of change of the volume of a cube with respect to its decreasing sides, we can use the derivative form as dy/dx.
It can also inspire researchers to find new applications for fractional calculus in the future. This page titled 4: Applications of Derivatives is shared under a CC BY-NC-SA 4.0 license and was authored, remixed, and/or curated by Gilbert Strang & Edwin Jed Herman (OpenStax) via source content that was edited to the style and standards of the LibreTexts platform; a detailed edit history is available upon request. The line \( y = mx + b \), if \( f(x) \) approaches it, as \( x \to \pm \infty \) is an oblique asymptote of the function \( f(x) \). Assume that f is differentiable over an interval [a, b]. Nie wieder prokastinieren mit unseren Lernerinnerungen.
Assign symbols to all the variables in the problem and sketch the problem if it makes sense. Calculus In Computer Science. Functions are said to be monotonic if they are either increasing or decreasing in their entire domain. When x= a, if f(x) f(a) for every x in the domain then f(x) has an Absolute Minimum value and the point a is the point of the minimum value of f. When x = a, if f(x) f(a) for every x in some open interval (p, q) then f(x) has a Relative Minimum value. How do I study application of derivatives? To find the tangent line to a curve at a given point (as in the graph above), follow these steps: For more information and examples about this subject, see our article on Tangent Lines.
Suppose change in the value of x, dx = x then. \], Now, you want to solve this equation for \( y \) so that you can rewrite the area equation in terms of \( x \) only:\[ y = 1000 - 2x. This application of derivatives defines limits at infinity and explains how infinite limits affect the graph of a function. Rolle's Theorem says that if a function f is continuous on the closed interval [a, b], differentiable on the open interval (a,b), andf(a)=f(b), then there is at least one valuecwheref'(c)= 0. It uses an initial guess of \( x_{0} \). Applications of derivatives in engineering include (but are not limited to) mechanics, kinematics, thermodynamics, electricity & magnetism, heat transfer, fluid mechanics, and aerodynamics.Essentially, calculus, and its applications of derivatives, are the heart of engineering. NCERT Solutions Class 12 Business Studies, NCERT Solutions Class 12 Accountancy Part 1, NCERT Solutions Class 12 Accountancy Part 2, NCERT Solutions Class 11 Business Studies, NCERT Solutions for Class 10 Social Science, NCERT Solutions for Class 10 Maths Chapter 1, NCERT Solutions for Class 10 Maths Chapter 2, NCERT Solutions for Class 10 Maths Chapter 3, NCERT Solutions for Class 10 Maths Chapter 4, NCERT Solutions for Class 10 Maths Chapter 5, NCERT Solutions for Class 10 Maths Chapter 6, NCERT Solutions for Class 10 Maths Chapter 7, NCERT Solutions for Class 10 Maths Chapter 8, NCERT Solutions for Class 10 Maths Chapter 9, NCERT Solutions for Class 10 Maths Chapter 10, NCERT Solutions for Class 10 Maths Chapter 11, NCERT Solutions for Class 10 Maths Chapter 12, NCERT Solutions for Class 10 Maths Chapter 13, NCERT Solutions for Class 10 Maths Chapter 14, NCERT Solutions for Class 10 Maths Chapter 15, NCERT Solutions for Class 10 Science Chapter 1, NCERT Solutions for Class 10 Science Chapter 2, NCERT Solutions for Class 10 Science Chapter 3, NCERT Solutions for Class 10 Science Chapter 4, NCERT Solutions for Class 10 Science Chapter 5, NCERT Solutions for Class 10 Science Chapter 6, NCERT Solutions for Class 10 Science Chapter 7, NCERT Solutions for Class 10 Science Chapter 8, NCERT Solutions for Class 10 Science Chapter 9, NCERT Solutions for Class 10 Science Chapter 10, NCERT Solutions for Class 10 Science Chapter 11, NCERT Solutions for Class 10 Science Chapter 12, NCERT Solutions for Class 10 Science Chapter 13, NCERT Solutions for Class 10 Science Chapter 14, NCERT Solutions for Class 10 Science Chapter 15, NCERT Solutions for Class 10 Science Chapter 16, NCERT Solutions For Class 9 Social Science, NCERT Solutions For Class 9 Maths Chapter 1, NCERT Solutions For Class 9 Maths Chapter 2, NCERT Solutions For Class 9 Maths Chapter 3, NCERT Solutions For Class 9 Maths Chapter 4, NCERT Solutions For Class 9 Maths Chapter 5, NCERT Solutions For Class 9 Maths Chapter 6, NCERT Solutions For Class 9 Maths Chapter 7, NCERT Solutions For Class 9 Maths Chapter 8, NCERT Solutions For Class 9 Maths Chapter 9, NCERT Solutions For Class 9 Maths Chapter 10, NCERT Solutions For Class 9 Maths Chapter 11, NCERT Solutions For Class 9 Maths Chapter 12, NCERT Solutions For Class 9 Maths Chapter 13, NCERT Solutions For Class 9 Maths Chapter 14, NCERT Solutions For Class 9 Maths Chapter 15, NCERT Solutions for Class 9 Science Chapter 1, NCERT Solutions for Class 9 Science Chapter 2, NCERT Solutions for Class 9 Science Chapter 3, NCERT Solutions for Class 9 Science Chapter 4, NCERT Solutions for Class 9 Science Chapter 5, NCERT Solutions for Class 9 Science Chapter 6, NCERT Solutions for Class 9 Science Chapter 7, NCERT Solutions for Class 9 Science Chapter 8, NCERT Solutions for Class 9 Science Chapter 9, NCERT Solutions for Class 9 Science Chapter 10, NCERT Solutions for Class 9 Science Chapter 11, NCERT Solutions for Class 9 Science Chapter 12, NCERT Solutions for Class 9 Science Chapter 13, NCERT Solutions for Class 9 Science Chapter 14, NCERT Solutions for Class 9 Science Chapter 15, NCERT Solutions for Class 8 Social Science, NCERT Solutions for Class 7 Social Science, NCERT Solutions For Class 6 Social Science, CBSE Previous Year Question Papers Class 10, CBSE Previous Year Question Papers Class 12, Arithmetic Progression Class 10 Questions, Trigonometric Functions - Domain And Range, Data Handling: Data Collection And Organization Of Data, CBSE Previous Year Question Papers Class 12 Maths, CBSE Previous Year Question Papers Class 10 Maths, ICSE Previous Year Question Papers Class 10, ISC Previous Year Question Papers Class 12 Maths, Differentiation and Integration of Determinants, System of Linear Equations Using Determinants, JEE Main 2023 Question Papers with Answers, JEE Main 2022 Question Papers with Answers, JEE Advanced 2022 Question Paper with Answers, f is increasing at [p, q] if f'(x) > 0 for each x (p, q), f is decreasing at [p, q] if f'(x) < 0 for each x (p, q), f is constant function in [p, q], if f'(x)=0 for each x (p, q). How do you find the critical points of a function? Let \( p \) be the price charged per rental car per day. 
4.0: In every case, to study the forces that act on different objects, or in different situations, the engineer needs to use applications of derivatives (and much more). WebSystems Engineering is an appropriate major for students who intend to pursue graduate studies in biomedical engineering. To maximize the area of the farmland, you need to find the maximum value of \( A(x) = 1000x - 2x^{2} \). 7. Solving related rates problems. WebThe current Research Topic highlights the new research work and review articles covering the design of bio-inspired hydrogels with diverse functions. Kamman Elementary Engineering Mathematics Application of Derivatives in Electrical Engineering page: 2/4 CurrentVoltage Relationships for Resistors, Capacitors, and Inductors The voltage across and the current through a resistor are related simply by its resistance. WebBachelors degree in Chemical or Mechanical Engineering and a minimum of 5 years of process/mechanical engineering experience in a petrochemical or refining facility is required. To maximize revenue, you need to balance the price charged per rental car per day against the number of cars customers will rent at that price. The limit of the function \( f(x) \) is \( - \infty \) as \( x \to \infty \) if \( f(x) < 0 \) and \( \left| f(x) \right| \) becomes larger and larger as \( x \) also becomes larger and larger. If \( f(c) \geq f(x) \) for all \( x \) in the domain of \( f \), then you say that \( f \) has an absolute maximum at \( c \). How much should you tell the owners of the company to rent the cars to maximize revenue? The peaks of the graph are the relative maxima. WebThe basic application of triple integral is finding mass of a solid. What relates the opposite and adjacent sides of a right triangle? Solving the initial value problem \[ \frac{dy}{dx} = f(x), \mbox{ with the initial condition } y(x_{0}) = y_{0} \] requires you to: first find the set of antiderivatives of \( f \) and then. The key terms and concepts of antiderivatives are: A function \( F(x) \) such that \( F'(x) = f(x) \) for all \( x \) in the domain of \( f \) is an antiderivative of \( f \). is a recursive approximation technique for finding the root of a differentiable function when other analytical methods fail, is the study of maximizing or minimizing a function subject to constraints, essentially finding the most effective and functional solution to a problem, Derivatives of Inverse Trigonometric Functions, General Solution of Differential Equation, Initial Value Problem Differential Equations, Integration using Inverse Trigonometric Functions, Particular Solutions to Differential Equations, Frequency, Frequency Tables and Levels of Measurement, Absolute Value Equations and Inequalities, Addition and Subtraction of Rational Expressions, Addition, Subtraction, Multiplication and Division, Finding Maxima and Minima Using Derivatives, Multiplying and Dividing Rational Expressions, Solving Simultaneous Equations Using Matrices, Solving and Graphing Quadratic Inequalities, The Quadratic Formula and the Discriminant, Trigonometric Functions of General Angles, Confidence Interval for Population Proportion, Confidence Interval for Slope of Regression Line, Confidence Interval for the Difference of Two Means, Hypothesis Test of Two Population Proportions, Inference for Distributions of Categorical Data. \].
To inquire about the program, students should email reuengineeringforhealthcare@mae.ufl.edu. b If there exists an interval, \( I \), such that \( f(c) \leq f(x) \) for all \( x \) in \( I \), you say that \( f \) has a local min at \( c \). Create the most beautiful study materials using our templates. Also learn how to apply derivatives to approximate function values and find limits using LHpitals rule. One of the most common applications of derivatives is finding the extreme values, or maxima and minima, of a function. WebDifferentials are the core of continuum mechanics.
How can you identify relative minima and maxima in a graph? 
Find the max possible area of the farmland by maximizing \( A(x) = 1000x - 2x^{2} \) over the closed interval of \( [0, 500] \). Iff'(x) is negative on the entire interval (a,b), thenfis a decreasing function over [a,b]. Unit 5: Analyzing functions . Well, this application teaches you how to use the first and second derivatives of a function to determine the shape of its graph. WebThese measurement techniques offer different advantages and limitations, and the choice of method depends on the specific application, desired accuracy, and experimental setup. Once you learn the methods of finding extreme values (also known collectively as extrema), you can apply these methods to later applications of derivatives, like creating accurate graphs and solving optimization problems. In previous classes, you must have learned to find the derivative of different functions, like, trigonometric functions, implicit functions, logarithm functions, etc. The Applications Engineer is the primary technical resource for the field sales force and is responsible for actively driving and managing the sale process of the technology evaluation.Working in conjunction with the sales team as An antiderivative of a function \( f \) is a function whose derivative is \( f \). 
StudySmarter is commited to creating, free, high quality explainations, opening education to all. de Barros 1, A. Pascoal 2, E. de Sa 3 1- Department of Mechatronics Engineering and Mechanical Systems, University of So Paulo. WebJob Description:. Building on the applications of derivatives to find maxima and minima and the mean value theorem, you can now determine whether a critical point of a function corresponds to a local extreme value. If \( f' \) has the same sign for \( x < c \) and \( x > c \), then \( f(c) \) is neither a local max or a local min of \( f \). If a function \( f \) has a local extremum at point \( c \), then \( c \) is a critical point of \( f \). Corollary 1 says that if f'(x) = 0 over the entire interval [a, b], then f(x) is a constant over [a, b]. Suppose \( f'(c) = 0 \), \( f'' \) is continuous over an interval that contains \( c \). Find the critical points by taking the first derivative, setting it equal to zero, and solving for \( p \).\[ \begin{align}R(p) &= -6p^{2} + 600p \\R'(p) &= -12p + 600 \\0 &= -12p + 600 \\p = 50.\end{align} \]. 6.5: Physical Applications of Integration In this section, we examine some physical applications of integration. WebApplications of derivatives in engineering include (but are not limited to) mechanics, kinematics, thermodynamics, electricity & magnetism, heat transfer, fluid In physics, the derivative of the displacement of a moving body with respect to time is the velocity. Engineering Application Optimization Example. WebEquations involving highest order derivatives of order one = 1st order differential equations Examples: Function (x)= the stress in a uni-axial stretched tapered metal rod (Fig. If \( f'(x) < 0 \) for all \( x \) in \( (a, b) \), then \( f \) is a decreasing function over \( [a, b] \). the command filters are introduced to limit the magnitude of the virtual control and to calculate the derivative of the virtual control, respectively. You find the application of the second derivative by first finding the first derivative, then the second derivative of a function. 
Since the area must be positive for all values of \( x \) in the open interval of \( (0, 500) \), the max must occur at a critical point.
